
// 소수: 소쑤(발음) -> 1과 자기 자신으로 밖에 나눠지지 않는 자연수 (=약수가 1과 자기 자신 밖에 없음)
// 1) 소수는 1보다 커야 한다.
// 2) 짝수는 소수가 아니다. (단, 2는 소수다.)
// 3) 어떤 수를 3부터 자기 자신 전까지의 수로 나눠서 나누어 떨어지면 소수가 아니다.
function isPrime(num) {
// 1이면 소수가 아니다.
if (num === 1) {
return false;
}
// 짝수는 소수가 아니지만, 2는 소수다.
if (num === 2) {
return true;
}
// 짝수는 소수가 아니다.
if (num % 2 === 0) {
return false;
}
// 1부터 자기 자신(num) 전까지 for문으로 반복하면서 나누어 떨어지는 경우가 있으면 소수가 아님
for (let i = 3; i < num; i++) {
if (num % i === 0) {
return false;
}
}
// 이외에는 나머지는 다 소수
return true;
}
제곱근 Math.sqrt() 을 사용한 답
- n이 소수가 아닐 때
N = a*b
- n이 소수일 때 (1과 자신만을 약수로 가짐으로)
a와 b의 관계식은 a <= b 이다.
(만약 a > b 이면 두 수를 바꿔서 b <= a 라고 표현할 수 있다.)
a와 b의 차이가 최소로 날 때 그 값은 √n*√n = n 이 나온다.
따라서 n이 axb로 표현될 수 있고, a <= b일 때, b의 최소값이며 a의 최대값은 √n이다.
- a가 √n보다 크게 되면, a*b > n
- b가 √n보다 작게 되면, a*b < n
- 따라서 a <= b일 때, a <= √n, b >=√n이다.
a와 b의 차이가 가장 작은 경우는 a와 b가 서로 √n이 되는 경우이다. 그러므로 √n까지만 반복해보면 이 수가 소수인지 알 수 있다.
위의 말을 예를 들어 쉽게 설명하자면 다음과 같다.
n = 36이라고 가정해보자.
36의 약수는 1, 2, 3, 4, 6, 9, 12, 18, 36 이다.
이는 1x36, 2x18, 3x12, 4x9, 6x6의 결과이다.
이들은 반비례 관계로 몫이 커지면 나누는 값이 작아지거나, 나누는 값이 커지면 몫이 작아진다. n의 절반(제곱근)까지 계산하게 되면 이후 몫과 나누는 값은 반대로 바뀐다.
- 따라서 n의 제곱근까지, 그러니까 a와 b가 서로 √n이 될 때 까지만 반복해보면 이 수가 소수인지 알 수 있다.
단, 제곱근으로 구할 시 3, 5, 7의 제곱근은 " Math.sqrt(9) = 3" 보다 더 작다는 것을 염두해 두어야 한다.
// 방법2
function isPrime(num) {
if(num <= 1) { // 음수와 1은 소수가 아니다
return false;
}
// 2는 짝수 중 유일한 소수이다
if( num % 2 === 0) {
return num === 2 ? true : false;
}
// 이제 num이 홀수 일때 다른 수에 나눠지는지 판별한다
// Math.sqrt(num) 즉, √num까지 나눠 떨어지는지 검사한다
// 원리는 아래글 "에라토스테네스의 체" 참고
const sqrt = parseInt(Math.sqrt(num));
for( let divider = 3; divider <= sqrt; divider += 2) {
if(num % divider === 0) {
return false;
}
}
return true;
}에라토스테네스의 체

1을 제외하고 2부터 N까지 자신을 제외하고 순차적으로 자신의 배수들을 지워가면 결국에는 소수들만 남는다는 원리이다. n까지가 아니라 √n까지만 검사해도 결과는 같다.
예를 들어 N = 25 이라고 가정해보자.
- 1은 소수가 아니기 때문에 2부터 실행한다.
- 2를 제외하고 2의 배수를 모두 제거한다. [4,6,8,10,12,14,16,18,20...제거]
- 3을 제외하고 3의 배수를 모두 제거한다. [9,15,21,24...제거] _6,18... 등은 2의 배수에서 이미 제거됨
- 4는 이미 삭제되었다.
- 5를 제외하고 5의 배수를 모두 제거한다[25,35,45,55... 제거]____(5의 제곱이 나오기 전까지 모든 5의 배수는 이미 삭제되었다)
- 6은 이미 삭제되었다.
따라서 √25(5)까지만 검사하면 된다. √25(5)이후의 배수들은 이미 삭제되었기 때문이다.
(여기서 n은 25라 가정 , 1부터 25까지의 5의 배수는 25를 제외하고 이미 지워진 상태이다 )
function isPrime(num) {
if (num === 1) {
return false;
}
if (num === 2) {
return true;
}
if (num % 2 === 0) {
return false;
}
let sqrt = Math.sqrt(num);
for (let i = 2; i <= sqrt; i++) {
// 어떤 수의 약수는 제곱근을 중심으로 대칭을 이룬다. -> 제곱근까지만 약수를 찾아도 소수를 찾을 수 있음
// ex) num이 12일 때,
// 1 * 12, 2 * 6, 3 * 4, 12의 제곱근 * 12의 제곱근, 4 * 3, 6 * 2, 12 * 1
if (num % i === 0) {
return false;
}
}
return true;
}

function listPrimes(num) {
// 9번은 소수인지 여부를 리턴 (boolean)
// 10번은 num보다 작은 소수를 문자열 형태로 나열해서 리턴
// ex) num = 12, '2-3-5-7-11'
// 문제에서 이중반복문 쓰라고 친절하게 안내
// 첫번째 반복문: 3부터 num까지 탐색하는 반복문 (이 수가 소수인가 아닌가)
// 두번째 반복문: 첫번째 반복문의 수를 소수인지 판단하는 반복문(9번 문제)
// 2만 아니면 홀수만 탐색해도 되는데...? 시간이 짧아지지 않을까? 2는 넣고 시작
let result = '2';
for(let prime = 3; prime <= num; prime += 2) {
// 이게 소수인지? -> 17번 문제.
// 18번은 찾아서 result에 더해 주어야 하므로, 판단할 수 있는 변수가 필요하다.
let isPrime = true;
let sqrt = Math.sqrt(prime);
for(let i = 3; i <= sqrt; i += 2) {
if (prime % i === 0) {
isPrime = false;
// 이미 소수인거 밝혀졌으면 굳이 나머지 더 할 필요가 없음 -> break
break;
// prime = 3일때 prime보다 작은 홀수 -> 소수임
// prime = 5, i = 3, prime % i === 2 소수 아님
// prime = 7, i = 3, prime % i === 1 소수
// prime = 7, i = 5, prime % i === 2 소수
// prime = 9, i = 3, prime % i === 0 소수 아님
// ...
}
}
if (isPrime) { // 만약 약수를 찾지 못했다면, 소수이므로 result에 붙여준다.
result = `${result}-${prime}`
}
}
// result를 리턴한다.
return result;
}function listPrimes(num) {
// 9번은 소수인지 여부를 리턴 (boolean)
// 10번은 num보다 작은 소수를 문자열 형태로 나열해서 리턴
// ex) num = 12, '2-3-5-7-11'
// 문제에서 이중반복문 쓰라고 친절하게 안내
// 첫번째 반복문: 3부터 num까지 탐색하는 반복문 (이 수가 소수인가 아닌가)
// 두번째 반복문: 첫번째 반복문의 수를 소수인지 판단하는 반복문(9번 문제)
// 2만 아니면 홀수만 탐색해도 되는데...? 시간이 짧아지지 않을까? 2는 넣고 시작
let result = '2';
for(let prime = 3; prime <= num; prime += 2) {
// 이게 소수인지? -> 17번 문제.
// 18번은 찾아서 result에 더해 주어야 하므로, 판단할 수 있는 변수가 필요하다.
let isPrime = true;
for(let i = 3; i < prime; i += 2) {
if (prime % i === 0) {
isPrime = false;
// 이미 소수인거 밝혀졌으면 굳이 나머지 더 할 필요가 없음 -> break
break;
// prime = 3일때 prime보다 작은 홀수 -> 소수임
// prime = 5, i = 3, prime % i === 2 소수 아님
// prime = 7, i = 3, prime % i === 1 소수
// prime = 7, i = 5, prime % i === 2 소수
// prime = 9, i = 3, prime % i === 0 소수 아님
// ...
}
}
if (isPrime) { // 만약 약수를 찾지 못했다면, 소수이므로 result에 붙여준다.
result = `${result}-${prime}`
}
}
// result를 리턴한다.
return result;
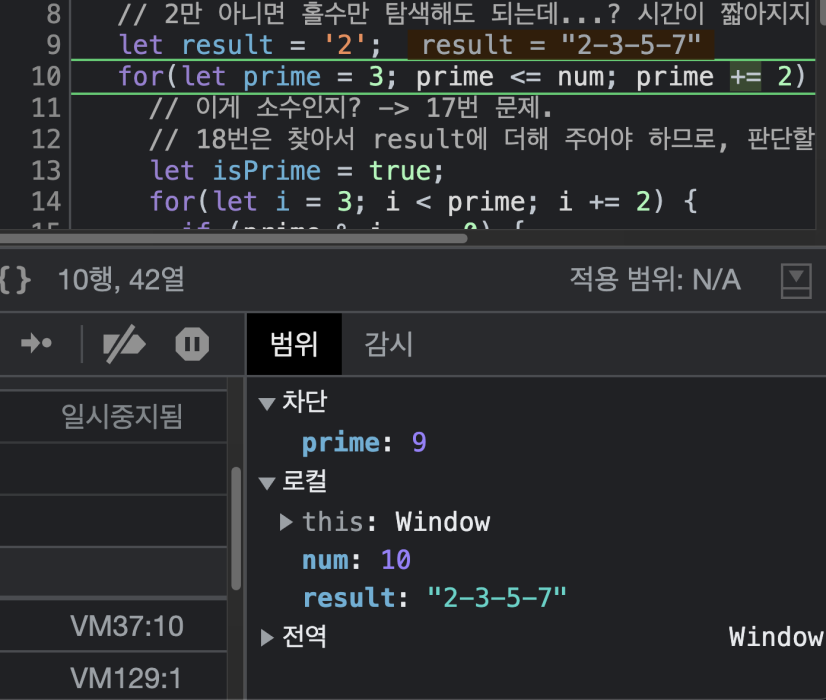
}- break를 빼도 테스트는 통과가 된다. break문이 있는 이유는 어떤 수가 소수가 아니라고 밝혀졌음에도 불필요한 과정이 진행되는 것을 방지하기 위함이다.
-
예를 들어 prime이 9일 경우, 3으로 나눴을 때 나누어 떨어지므로 소수가 아니라고 밝혀지게 되는데, break문이 없으면 5와 7로도 나누어 떨어지는지 확인하게 된다. 이미 isPrime이 false가 되어 있으므로 5와 7로 나눈 결과는 의미가 없는데 불필요한 연산을 한다는 뜻이다.
-
break문이 있으면 9가 3으로 나누어 떨어진 순간 내부 반복문이 종료가 된다.
-
그리고 외부 반복문 내부에 있는 isPrime 변수에 true가 할당되면서 다음 숫자(11)를 소수인지 판별하게 된다.<9를 3으로 나눠서 isPrime이 false가 되었음에도 i가 5가 되어 다음 과정을 확인하는 모습>
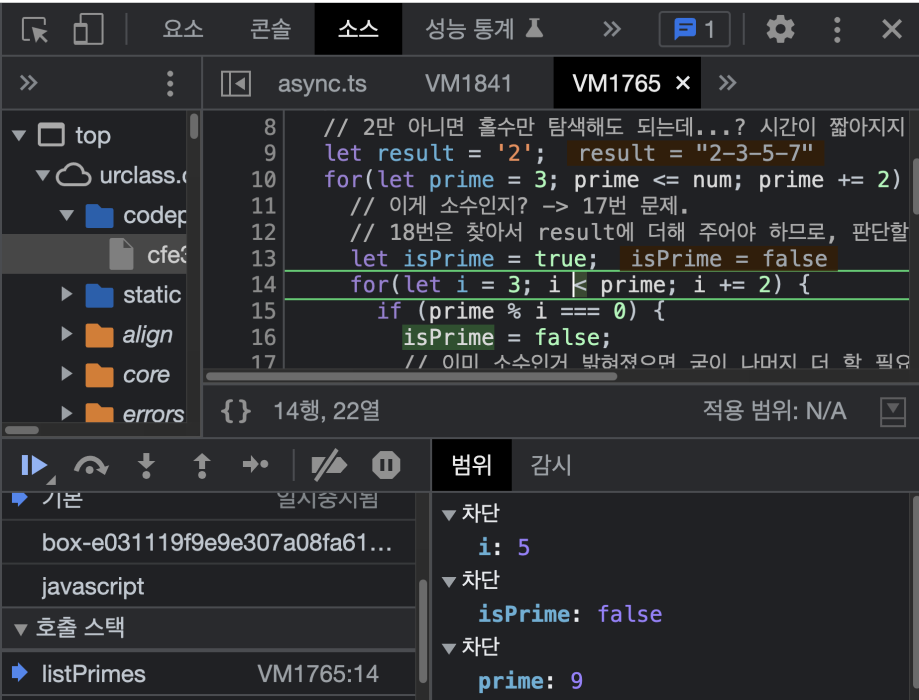
break문을 사용하면 i가 5가 되지 않고 내부 반복문이 종료됩니다.
728x90
'FE > JavaScript' 카테고리의 다른 글
| [JS] 원시 자료형과 참조 자료형 (0) | 2023.03.02 |
|---|---|
| [JS] 원본 배열을 변경하는 / 변경하지 않는 배열 메서드 (0) | 2023.03.01 |
| [JS] 객체 - 개념 정리 (0) | 2023.02.28 |
| [JS] 객체 Object (0) | 2023.02.27 |
| (JS) 배열의 반복 & 배열 메서드 (0) | 2023.02.27 |